86.0576519035213 explained
(and why it is actually wrong)
When asking
around for ideas for cool tools to make, Sjoerd De Jong told me about a problem
he had with the bend modifier in 3ds Max. He always had to fix it manual which
was tedious. When applying a bend modifier on a prop with a power of 2 height, the endresults
width was not dividable by 2 and thus not on the grid (UDK grid, every 8 units) However Sjoerd found a solution which he posted on his site
-
When you got modular on grid meshes in Max/Maya, and you bend them
90/180/270 degrees, their
ends are never ever on grid, even though the original
mesh was perfectly on grid. Most people, that
included me, would in that case
manually move the vertices on one end and snap them to the grid.
That gets very
tedious to do very fast though.
I just found out that if you take the length of the mesh, divided by
exactly 86.0576519035213, and
then take the result of that division and use
that to offset the center of the bend deform with into the
opposite direction
the mesh bends, then the end of that mesh will be exactly on grid!
So for example,
a 1024 long mesh that bends needs to have its bend pivot point
offset by 11.899 units and it will end
up exactly on the grid.
-
So I decided to give this a test in 3ds max. After applying the bend modifier I saw that indeed, the last vertex did not ended on a power of 2 grid. So I tried Sjoerd his fix.
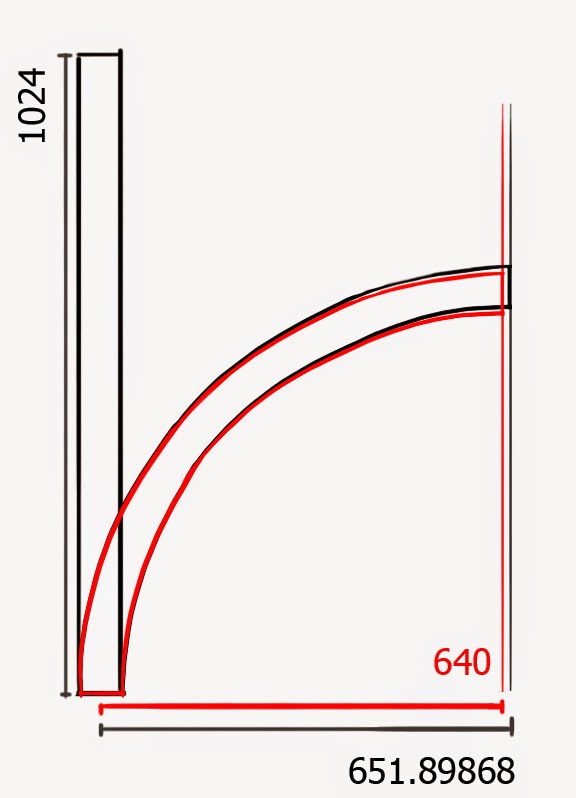1024/86.0576519035213 = 11.899After offsetting with 11.899 the width was 640
Success!
I asked Sjoerd
where he got the number but he couldn’t remember. And no one on the internet knew
why 86.0576519035213 gave that result. But it worked so I just accepted it and
decided to make a script for it.
However, after
creating a script that added the correct offset based on the direction and the angle,
I discovered it only worked for 90 degree angles. The angles 180,270 and 360
didn´t end up on the grid. Did I make a mistake?
I tried various sizes and tried to do it
manual, but it all gave the same result.
86.0576519035213 wasn’t the perfect number after all.
86.0576519035213 wasn’t the perfect number after all.
If I wanted to make it work for all angles , I had to figure out why dividing by 86.0576519035213 gave the correct result for 90 degree angles.
I assumed the bend modifier tried to keep the
same distance on the arc of the circle.
If this was true I knew I would be able to find a way, else I would make the script only for 90 degrees.
If it’s a circle, we can say width = radius
O = the circumference of a circle:
If this was true I knew I would be able to find a way, else I would make the script only for 90 degrees.
If it’s a circle, we can say width = radius
O = the circumference of a circle:
O = 2 * π * r
We only have a 90 degree
angle, or 1 fourth of the normal circumference
h = height
O = 4 * h
If we equal
both O formula
4 * h = 2 * π * r
r = 2 * h / π
When we
fill in our values we see that the formula is correct
r = 2 * 1024 / π = 651.89868
Now that we
know how to calculate the radius, we can use this to calculate in the reverse
order.
From Sjoerds
method we know that we have to move the center of the bendmodifier.
Since we move it in the opposite direction, this is the same as making the initial radius smaller.
This means we subtract, or add a negative number to the initial radius.
This is where it gets confusing:
we have the initial bad radius : 651.89868 and the final radius : 640
when we move the center with the correct offset we get the final radius :
Since we move it in the opposite direction, this is the same as making the initial radius smaller.
This means we subtract, or add a negative number to the initial radius.
This is where it gets confusing:
we have the initial bad radius : 651.89868 and the final radius : 640
when we move the center with the correct offset we get the final radius :
rf = final radius
r + offset = rf
offset = rf – r
Testing
this in 3ds Max
We have a 1024 high cube, which results in a 651.89868 radius
lets try to make this into a 512 radius:
We have a 1024 high cube, which results in a 651.89868 radius
lets try to make this into a 512 radius:
rf = r + offset = 651.89868 + -11.899 = 640
With this
confirmed we now know how to calculate the correct offset with the radius.
Since we also know how to calculate the radius, we can put them together:
Since we also know how to calculate the radius, we can put them together:
offset = rf – r = rf - 2 * h / π
Using this
formula we can choose any final radius and get it´s offset.
This is still only for 90 degrees, but using this we can easily get the other degrees their formula.
This is still only for 90 degrees, but using this we can easily get the other degrees their formula.
But one
question remains unanswered, why did the number 86.0576519035213 work for 90
degrees? Now that we have the formula to calculate any radius, and sjoers
original formula, we can find out. Let us pretend we don’t know this constant,
and want to calculate it.
# = constant
h / # = offset
r + offset = rf
2 * h / π + h / # = rf
h / # = rf - 2 * h / π
# = h / ( rf - 2 * h / π )
Let´s put
our values in there and use wolfram to calculate the most exact possible result
the final radius Sjoerd had as result was 640 for a 1024 height, and 320 for a 512
the final radius Sjoerd had as result was 640 for a 1024 height, and 320 for a 512
# = 1024 / (640 – 2 * 1024 / π ) = -86.0602056878460272632506284428750874459128685735009
This is very
close to our original number, is it just coincidence?
# =512 / (320 – 2 * 512 / π ) = -86.0602056878460272632506284428750874459128685735009
No coincidence. And we can
easily see in the formula that they just multiply all elements with 2, which
cancel each other, thus always leading to the same result. Since the relationship between 1024 / 620 and 512 / 320 is constant, we can simplify this to 8 and 5.The height is always a power of 2, and the end result width a multiplication of 5 and 2
So to come
back on our question, why did 86.0576519035213 work and how did someone found
it.
It works because it is almost the same as our result so it gives the same result if using it to calculate the offset. Since floating points get rounded on the computer. And how did someone find it? I guess through trial and error, since it is not perfect, but I will never know for sure.
It works because it is almost the same as our result so it gives the same result if using it to calculate the offset. Since floating points get rounded on the computer. And how did someone find it? I guess through trial and error, since it is not perfect, but I will never know for sure.
But now
that we know the formula we don’t need the number anymore, however we still
have the option to use it, or can calculate the correct number for the other
angles.
180 degrees
In a 180
degree bend the width is 2 times the radius, and half of the circumference is
the height:
O = 2 * r * π = 2 * h
O / 2 = r * π = h
r = h / π
2 r = width = 2 * h / π
Here we get
the same formula as before again, even though the width proportion to the
radius changed, the height changed in a similar way countering each other.
Let´s now
calculate the offset. The offset is how much we move the center. Since the
width is 2 times the radius, the width will be detracted with 2 times the
offset.
2 * r + offset * 2 = width
offset = ( width – 2 * r ) / 2
offset = width / 2 – h / π
The offset
formula is half of the 90 degree offset formula.
h / # = offset
2 * r + offset * 2 = width
2 * h / π +2 * h / # = width
2 * h / # = width – 2 * h / π
# = h / ( width - 2 * h / π ) / 2
The constant
formula is half of the 90 degree constant formula.
270 degrees
Since it
contains 3 parts, it does not nicely divide by 2. The height is 3 fourth of the
circumference. The width is 2 times the radius. So we can use the 180 degree
formula and input height/3*2 as the height.
O = 2 * π * r
O / 4 * 3 = h
h = 2 * π * r / 4 * 3
h = 3 * π * r / 2
r = 2 * h / ( 3 * π )
width = 2 * r
width = 4 * h / ( 3 * π )
2 * r + offset * 2 = width
offset = ( width – 2 * r ) / 2
offset = width / 2 – 2 * h / ( 3 * pi )
h / # = offset
O / 4 * 3 = h
h = 2 * π * r / 4 * 3
h = 3 * π * r / 2
r = 2 * h / ( 3 * π )
width = 2 * r
width = 4 * h / ( 3 * π )
2 * r + offset * 2 = width
offset = ( width – 2 * r ) / 2
offset = width / 2 – 2 * h / ( 3 * pi )
h / # = offset
2 * r + offset * 2 = width
offset * 2 = width – 2 * r = width – 2 * h * 3 / ( 2 * π )
2 * h * 3 / ( 2 * π ) + 2 * h / # = width
h * 3 / π + 2 * h / # = width
# = 2 * h / (width – h * 3 / π )
Testing this
in 3ds Max shows us that using the constant to get a nice multiplication of 5
and 2 changes the size quite a lot. Since there is such a big difference
between the initial and final radius it would be wiser to solve it in a
different way. For example divide by a power of 2 and remove the remainder,
then use the quotient and multiply it back with the power of 2 that you used.
To get even less deformation, round the remainder up and add one to the quotient if the remainder is more than half of the power of 2.
To get even less deformation, round the remainder up and add one to the quotient if the remainder is more than half of the power of 2.
I would
even suggest this method for every other degree since it is more accurate and
adapts to the grid size, giving the user more control over his modular pieces.
360 degrees
The height
is the same as the circumference. The width is 2 times the radius, just like the
180 degrees. This means we can input half of our height in the 180 degree
formula to get the result, and this also means the constant is halved again.
-21.5150514219615068158126571107187718614782171433752
Now knowing all of this, it easy to automate the whole proces! This will make creating modular curved pieces much easier for the artist, which was my final goal. This was quite different from my usual process, which barely uses mathematics and is more pure scripting and automating. I decided to write down my though process so people can understand why this number was used and how they can use it for their own solutions.
